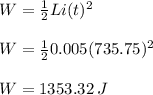Question

the voltage across a 5mH inductor is 5[1-exp(-0.5t)]V. Calculate the current through the inductor and the energy stored in the inductor at t=2 seconds

Answer 1

Given Information:

Inductance = L = 5 mH = 0.005 H

Time = t = 2 seconds

Required Information:

Current at t = 2 seconds = i(t) = ?

Energy at t = 2 seconds = W = ?

Answer:

Current at t = 2 seconds = i(t) = 735.75 A

Energy at t = 2 seconds = W = 1353.32 J

Step-by-step explanation:

The voltage across an inductor is given as

`V(t) = 5(1-e^(-0.5t))`

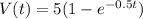
The current flowing through the inductor is given by

`i(t) = (1)/(L) \int_0^t \mathrm{V(t)}\,\mathrm{d}t \,+ i(0)`

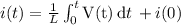
Where L is the inductance and i(0) is the initial current in the inductor which we will assume to be zero since it is not given.

`i(t) = (1)/(0.005) \int_0^t \mathrm{5(1-e^(-0.5t)}) \,\mathrm{d}t \,+ 0\\\\i(t) = 200 \int_0^t \mathrm{5(1-e^(-0.5t)}) \,\mathrm{d}t \\\\i(t) = 200 \: [ {5\: (t + (e^(-0.5t))/(0.5))]_0^t \\i(t) = 200*5\: \: [ { (t + 2e^(-0.5t) + 2 )] \\`

`i(t) = 1000t +2000e^(-0.5t) -2000\\`

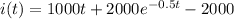
So the current at t = 2 seconds is

`i(t) = 1000(2) +2000e^(-0.5(2)) -2000\\\\i(t) = 735.75 \: A`

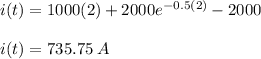
The energy stored in the inductor at t = 2 seconds is

`W = (1)/(2)Li(t)^(2)\\\\W = (1)/(2)0.005(735.75)^(2)\\\\W = 1353.32 \:J`