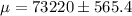Question

To estimate LaTeX: \muμ, the mean salary of full professors at American colleges and universities, you obtain the salaries of a random sample of 400 full professors. The sample mean is LaTeX: \bar{x} = $73,220 x ¯ = $ 73 , 220 and the sample standard deviation is s = $4400. A 99% confidence interval for LaTeX: \mu μ is Group of answer choices

A. 73220 +/- 11440

B. 73220 +/- 568

C. 73220 +/- 431

D. 73220 +/- 28.6

Answer 1

99% confidence interval for
`\mu = 73220 \pm 565.4`

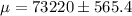
Explanation:

Sample mean =
`\bar{x} =73220`

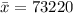
Standard deviation = s = 4400

Z at 99% confidence level = 2.57

Sample = n = 400

Formula of confidence interval :
`\bar{x} \pm Z * (s)/(√(n))`

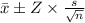
Substitute the values in the formula :

So,99% confidence interval for
`\mu = 73220 \pm 2.57 ((4400)/(√(400)))`

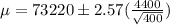
99% confidence interval for
`\mu = 73220 \pm 565.4`