Question

Two lasers are shining on a double slit, with slit separation d. Laser 1 has a wavelength of d/20, whereas laser 2 has a wavelength of d/15. The lasers produce separate interference patterns on a screen a distance 4.80m away from the slits.

Part A


Which laser has its first maximum closer to the central maximum?


Part B


What is the distance \Delta _y__max-max_ between the first maxima (on the same side of the central maximum) of the two patterns?


Express your answer in meters.


Part C


What is the distance \Delta _y__max-max_ between the second maximum of laser 1 and the third minimum of laser 2, on the same side of the central maximum?


Express your answer in meters.

Answer 1

A) first laser

B) 0.08m

C) 0.64m

Step-by-step explanation:

To find the position of the maximum you use the following formula:

`y=(m\lambda D)/(d)`

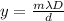
m: order of the maximum

λ: wavelength

D: distance to the screen = 4.80m

d: distance between slits

A) for the first laser you use:

`y_1=((1)(d/20)(4.80m))/(d)=0.24m\\`

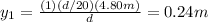
for the second laser:

`y_2=((1)(d/15)(4.80m))/(d)=0.32m`

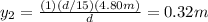
hence, the first maximum of the first laser is closer to the central maximum.

B) The difference between the first maximum:

`\Delta y=y_2-y_1=0.32m-0.24m=0.08m=8cm`

hence, the distance between the first maximum is 0.08m

C) you calculate the second maximum of laser 1:

`y_(m=2)=((2)(d/20)(4.80m))/(d)=0.48m`

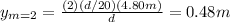
and for the third minimum of laser 2:

`y_(minimum)=((m+(1)/(2))(\lambda)(D))/(d)\\\\y_(m=3)=((3+(1)/(2))(d/15)(4.80m))/(d)=1.12m`

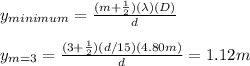
Finally, you take the difference:

`1.12m-0.48m=0.64m`

hence, the distance is 0.64m