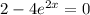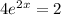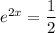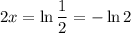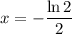Question

Pleeease open the image and hellllp me

Answer 1

1. Rewrite the expression in terms of logarithms:

`y=x^x=e^(\ln x^x)=e^(x\ln x)`

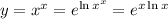
Then differentiate with the chain rule (I'll use prime notation to save space; that is, the derivative of y is denoted y' )

`y'=e^(x\ln x)(x\ln x)'=x^x(x\ln x)'`

`y'=x^x(x'\ln x+x(\ln x)')`

`y'=x^x\left(\ln x+\frac xx\right)`

`y'=x^x(\ln x+1)`

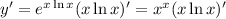
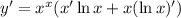
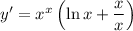
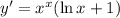
2. Chain rule:

`y=\ln(\csc(3x))`

`y'=\frac1{\csc(3x)}(\csc(3x))'`

`y'=\sin(3x)\left(-\cot^2(3x)(3x)'\right)`

`y'=-3\sin(3x)\cot^2(3x)`

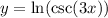
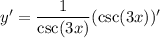
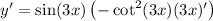
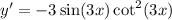
Since
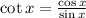`\cot x=(\cos x)/(\sin x)`, we can cancel one factor of sine:

`y'=-3(\cos^2(3x))/(\sin(3x))=-3\cos(3x)\cot(3x)`

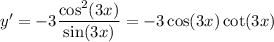
3. Chain rule:

`y=e^{e^(\sin x)}`

`y'=e^{e^(\sin x)}\left(e^(\sin x)\right)'`

`y'=e^{e^(\sin x)}e^(\sin x)(\sin x)'`

`y'=e^{e^(\sin x)+\sin x}\cos x`

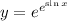
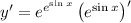
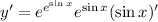
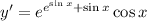
4. If you're like me and don't remember the rule for differentiating logarithms of bases not equal to e, you can use the change-of-base formula first:

`\log_2x=(\ln x)/(\ln2)`

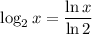
Then

`(\log_2x)'=\left((\ln x)/(\ln 2)\right)'=\frac1{\ln 2}`

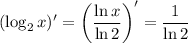
So we have

`y=\cos^2(\log_2x)`

`y'=2\cos(\log_2x)\left(\cos(\log_2x)\right)'`

`y'=2\cos(\log_2x)(-\sin(\log_2x))(\log_2x)'`

`y'=-\frac2{\ln2}\cos(\log_2x)\sin(\log_2x)`

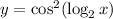
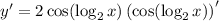
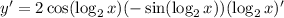
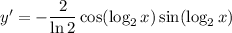
and we can use the double angle identity and logarithm properties to condense this result:

`y'=-\frac1{\ln2}\sin(2\log_2x)=-\frac1{\ln2}\sin(\log_2x^2)`

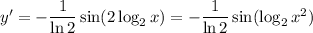
5. Differentiate both sides:

`\left(x^2-y^2+\sin x\,e^y+\ln y\,x\right)'=0'`

`2x-2yy'+\cos x\,e^y+\sin x\,e^yy'+\frac{xy'}y+\ln y=0`

`-\left(2y-\sin x\,e^y-\frac xy\right)y'=-\left(2x+\cos x\,e^y+\ln y\right)`

`y'=(2x+\cos x\,e^y\ln y)/(2y-\sin x\,e^y-\frac xy)`

`y'=(2xy+\cos x\,ye^y\ln y)/(2y^2-\sin x\,ye^y-x)`

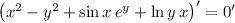
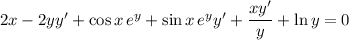
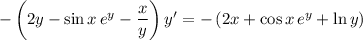
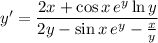
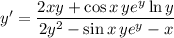
6. Same as with (5):

`\left(\sin(x^2+\tan y)+e^(x^3\sec y)+2x-y+2\right)'=0'`

`\cos(x^2+\tan y)(x^2+\tan y)'+e^(x^3\sec y)(x^3\sec y)'+2-y'=0`

`\cos(x^2+\tan y)(2x+\sec^2y y')+e^(x^3\sec y)(3x^2\sec y+x^3\sec y\tan y\,y')+2-y'=0`

`\cos(x^2+\tan y)(2x+\sec^2y y')+e^(x^3\sec y)(3x^2\sec y+x^3\sec y\tan y\,y')+2-y'=0`

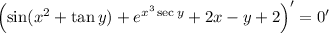
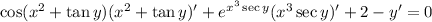
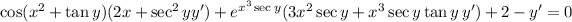
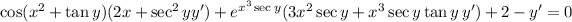
`y'=-(2x\cos(x^2+\tan y)+3x^2\sec y\,e^(x^3\sec y)+2)/(\cos(x^2+\tan y)\sec^2y+x^3\sec y\tan y\,e^(x^3\sec y)-1)`

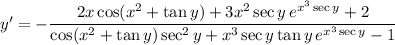
7. Looks like

`y=x^2-e^(2x)`

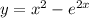
Compute the second derivative:

`y'=2x-2e^(2x)`

`y''=2-4e^(2x)`

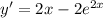
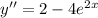
Set this equal to 0 and solve for x :

`2-4e^(2x)=0`

`4e^(2x)=2`

`e^(2x)=\frac12`

`2x=\ln\frac12=-\ln2`

`x=-\frac{\ln2}2`