Question

A 10-turn coil of wire having a diameter of 1.0 cm and a resistance of 0.30 Ω is in a 1.0 mT magnetic field, with the coil oriented for maximum flux. The coil is connected to an uncharged 3.0 μF capacitor rather than to a current meter. The coil is quickly pulled out of the magnetic field.

Afterward, what is the voltage across the capacitor?

Answer 1

The voltage across the capacitor = 0.8723 V

Step-by-step explanation:

From the question, it is said that the coil is quickly pulled out of the magnetic field. Therefore , the final magnetic flux linked to the coil is zero.

The change in magnetic flux linked to this coil is:

`\delta \phi = \phi _f - \phi _i`

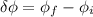
= 0 - BA cos 0°

`\delta \phi =-BA \\ \\ \delta \phi =-B( \pi r^2) \\ \\ \delta \phi =(1.0 \ mT)[ \pi ( (d)/(2) )^2]`

`\delta \phi =(1.0 \ mT)[ \pi ( (0.01)/(2) )^2]`

`\delta \phi = -7.85*10^8 \ Wb`

Using Faraday's Law; the induced emf on N turns of coil is;

`\epsilon = N |( \delta \phi)/(\delta t) |`

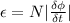
Also; the induced current I =
`( \epsilon)/(R)`

`( \delta q)/( \delta t) = (1)/(R) (N|(\delta \phi)/(\delta t ) |)`

`\delta q = (1)/(R) N|\delta \phi |`

`\delta q = (1)/(0.30) (10)| -7.85*10^8 \ Wb |`

`\delta q = 2.617*10^(-6) \ C`

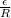
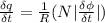
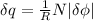
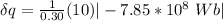
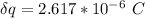
The voltage across the capacitor can now be determined as:

`\delta \ V =( \delta q)/(C)`

=
`( 2.617*10^(-6) \ C)/(3.0 \ *10^(-6) F)`

= 0.8723 V