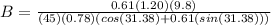Question

A 1.20 kg copper rod rests on two horizontal rails 0.78 m apart and carries a current of 45 A from one rail to the other. The coefficient of static friction between rod and rails is 0.61. What is the magnitude of the smallest magnetic field that puts the rod on the verge of sliding

Answer 1

B = 0.204T

Step-by-step explanation:

To find the value of the magnetic force you use the following formula:

`F_B=ILBsin\theta`

I: current of the copper rod = 45A

B: magnitude of the magnetic field

L: 0.78m

you assume that magnetic field B and current I are perpendicular between them.

The magnetic force must be, at least, equal to the friction force, that is:

`F_(f)=F_(B)\\\\\mu N=\mu Mg=ILB\\\\B=(\mu Mg)/(IL)`

M: mass of the rod = 1.20kg

μ: coefficient of static friction = 0.61

g: gravitational acceleration constant = 9.8m/s^2

By replacing the values of the parameters you obtain:

`B=((0.61)(1.20kg)(9.8m/s^2))/((45A)(0.78m))=0.204T`

Answer 2

The magnitude of the smallest magnetic field is
`B = 0.1744 \ T`

Step-by-step explanation:

From the question we are told that

The mass of the copper is
`m = 1.20 kg`

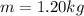
The distance of separation for the rails is
`d = 0.78 \ m`

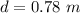
The current is
`I = 45 A`

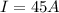
The coefficient of static friction is
`\mu = 0.61`

The force acting along the vertical axis is mathematically represented as

`F = mg - F_y`

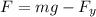
Where
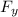`F_y` is the force acting on copper rod due to the magnetic field generated this is mathematically represented as

`F_y = I * d * B_1`

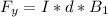
The magnetic field here is acting towards the west because according to right hand rule magnetic field acting toward the west generate a force acting in the vertical axis

So the equation becomes

`F = mg - I * d * B_1`

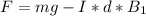
Here
`B_1 = B sin \theta`

`F = mg - I * d * Bsin(\theta )`

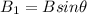
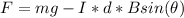
The in the horizontal axis is mathematically represented as

`F_H = ma + F_x`

Since the rod is about to move it acceleration is zero

Now
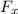`F_x` is the force acting in the horizontal direction due to the magnetic field acting downward this is because a according to right hand rule magnetic field acting downward generate a force acting in the horizontal positive horizontal direction. this mathematically represented as

`F_H = 0 + I * d * B_2`

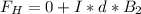
So the equation becomes

`F_H = I * d * B_2`

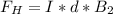
Here
`B_2 = B cos \theta`

`F_H = I * d * Bcos (\theta)`

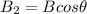
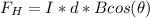
Now the frictional force acting on this rod is mathematically represented as

`F_F = \mu * F`

`F_F = \mu * (mg -( I * d * Bsin(\theta )))`

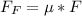
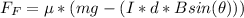
Now when the rod is at the verge of movement

`F_H = F_F`

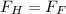
So
`I * d * Bcos (\theta) = \mu * (mg -( I * d * Bsin(\theta )))`

=>
`B = (\mu mg )/(I * d (cos \theta + \mu (sin \theta )))`

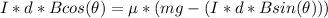
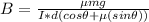
Now
`\theta` is the is the angle of the magnetic field makes with the vertical and the horizontal and this can be mathematically evaluated as

`\theta = tan^(-1) (\mu )`

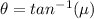
Substituting value

`\theta = tan^(-1) ( 0.61 )`

`\theta = 31.38^o`

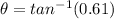
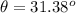
Substituting values into the equation for B

`B = (0.61 (1.20) (9.8))/((45) (0.78) (cos (31.38) + 0.61 (sin (31.38)) ))`

`B = 0.1744 \ T`