Question

You might need:

Calculator
Yasemin deposited $1000 into a savings account.
The relationship between the time, t, in years, since the account was first opened, and Yasemin's account
balance, B(t), in dollars, is modeled by the following function.
B(t) = 1000. 20.03
How many years will it take for Yasemin's account balance to reach $1500?
Round your answer, if necessary, to the nearest hundredth.

Answer 1

The number of years it will take for Yasemin's account balance to reach $1500 is 13.52 years.

Explanation:

Where the model of the relationship between the time, t, in years, since the account was first opened and the and the balance in Yasemin's account is presented as follows;

`B(t) = 1000 * e^((0.03 * t))`

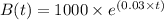
To find find out how many years it will take for Yasemin's account balance to reach $1500, we substitute B(t) = $1500 since we are told that after the years his account balance became $1500 as follows;

`\$ 1500 = 1000 * e^((0.03 * t))`

We now solve for t

`\$ 1500 = 1000 * e^((0.03 * t))\\\\(1500 )/(1000 ) = e^((0.03 * t))\\1.5 = e^((0.03 * t))\\\\ln(1.5) = ln (e^((0.03 * t)))\\\\ln(1.5) = (0.03 * t) * ln (e)\\\\\therefore ln(1.5) = (0.03 * t) \\\\t = (ln(1.5))/(0.03 ) = 13.52 \ years`

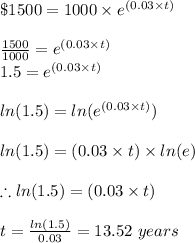
The number of years it will take for Yasemin's account balance to reach $1500 = 13.52 years.