Question

Find an equation equivalent to r = 10 sin theta rectangular coordinates.

Answer 1

x^2+y^2=10y

Explanation:

d on edg

Answer 2

We have been an equation in polar coordinates
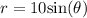`r=10\text{sin}(\theta)`. We are asked to write our equation in rectangular coordinates.

We know that the equation
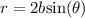`r=2b\text{sin}(\theta)` is equation of a circle with a radius
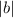`|b|` and center at
`(0,b)`.

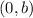Let us find the value of b.

`2b\text{sin}(\theta)=10\text{sin}(\theta)`

`\frac{2b\text{sin}(\theta)}{2\text{sin}(\theta)}=\frac{10\text{sin}(\theta)}{2\text{sin}(\theta)}`

`b=5`

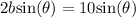
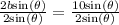
We know that equation of a circle in rectangular coordinates is
`(x-h)^2+(y-k)^2=r^2`

Since
`b=5`, so radius is 5 and center is at point (0,5).

`(x-0)^2+(y-5)^2=5^2`

`x^2+(y-5)^2=25`

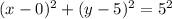
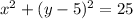
Therefore, our required equation would be
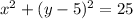`x^2+(y-5)^2=25`.