Answer:
The energy, that is dissipated in the resistor during this time interval is 153.6 mJ
Step-by-step explanation:
Given;
number of turns, N = 179
radius of the circular coil, r = 3.95 cm = 0.0395 m
resistance, R = 10.1 Ω
time, t = 0.163 s
magnetic field strength, B = 0.573 T
Induced emf is given as;
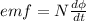
where;
ΔФ is change in magnetic flux
ΔФ = BA = B x πr²
ΔФ = 0.573 x π(0.0395)² = 0.002809 T.m²

According to ohm's law;
V = IR
I = V / R
I = 3.0848 / 10.1
I = 0.3054 A
Energy = I²Rt
Energy = (0.3054)² x 10.1 x 0.163
Energy = 0.1536 J
Energy = 153.6 mJ
Therefore, the energy, that is dissipated in the resistor during this time interval is 153.6 mJ