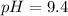Answer:
The pH is
Step-by-step explanation:
From the question we are told that
The volume of
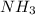 is
is
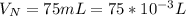
The concentration of
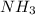 is
is

The concentration of
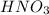 is
is
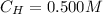
The volume of
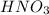 added is
added is
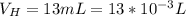
The base dissociation constant is
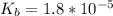
The number of moles of
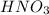 that was titrated can be mathematically represented as
that was titrated can be mathematically represented as
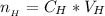
substituting values
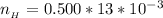
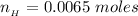
The number of moles of
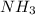 that was titrated can be mathematically represented as
that was titrated can be mathematically represented as
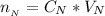
substituting values
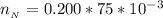
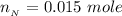
So from the calculation above the limited reactant is
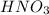
The chemical equation for this reaction is
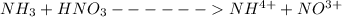
From the chemical reaction
1 mole of
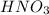 is titrated with 1 mole of
is titrated with 1 mole of
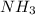 to produce 1 mole of NH^{4+}
to produce 1 mole of NH^{4+}
So
0.0065 moles of
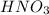 is titrated with 0.0065 mole of
is titrated with 0.0065 mole of
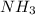 to produce 0.0065 mole of
to produce 0.0065 mole of

So
The remaining moles of
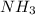 after the titration is
after the titration is
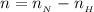
=>
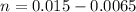
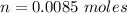
Now according to Henderson-Hasselbalch equation the pH of the reaction is mathematically represented as
![pH = pK_a + log [(NH_3)/(NH^(4+)) ]](https://img.qammunity.org/2021/formulas/chemistry/college/oecusyxn96snt6gpzyplbiyy6mtf3ufd56.png)
Where
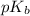 is mathematically represented as
is mathematically represented as
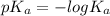
Now

Where
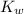 is the ionization constant of
is the ionization constant of
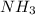 with value
with value

Hence
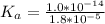
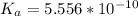
Substituting this into the equation
![pH = -log K_a + log [(NH_3)/(NH^(4+)) ]](https://img.qammunity.org/2021/formulas/chemistry/college/5fyeqhk2p0ehk48oni5be8vjzusy338jkz.png)
![pH = log [((NH_3)/(NH^(4+)) )/(K_a) ]](https://img.qammunity.org/2021/formulas/chemistry/college/jfssgz8llqsknszp0172m2j8qyoc71i24v.png)
substituting values
![pH = log [((0.0085)/(0.0065) )/(5.556*10^(-10)) ]](https://img.qammunity.org/2021/formulas/chemistry/college/rtfev4bnes4to5f9a2roaelhr2iff2c782.png)