Answer:
Vertical component of velocity is
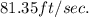
Horizontal component of velocity is
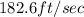 .
.
Explanation:
Horizontal component of velocity is defined as:
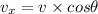
Vertical component of velocity is defined as:
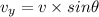
Where
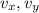 are the horizontal and vertical components of velocity.
are the horizontal and vertical components of velocity.
 is the actual velocity and
is the actual velocity and
 is the angle with horizontal axis at which the object was thrown.
is the angle with horizontal axis at which the object was thrown.
Here, we are provided with the following:
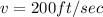
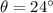

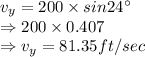
So, Vertical component of velocity is
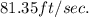
Horizontal component of velocity is
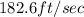 .
.