Answer:
The volume of the roof rounded to the nearest tenths is 2226.56 ft³
Explanation:
We note that the shape of the cross section of the roof is that of a triangle, whereby the volume in this case is the product of the length of the roof and the area of the triangular cross section as follows;
Area of the roof triangular cross section =
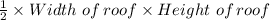
Width of the roof, W = 14.25 ft
Height of the roof, h = 2.5 ft
∴ Roof cross sectional area =
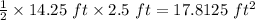
Length of roof = 125 ft
Hence, volume of root = Roof cross sectional area × Roof length
∴ Volume of root = 17.8125 ft² × 125 ft = 2226.56 ft³
The volume of the roof rounded to the nearest tenths = 2226.56 ft³.