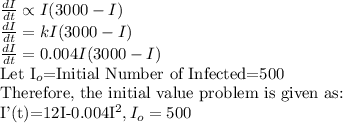Question

A disease is spreading throughout a community of 3,000 people at a rate (measured in number infected per day) proportional to the product of number of people infected and the number of people not yet infected, with constant of proportionality k = 0.004. Initially, 500 people are infected. Write an initial value problem.

Answer 1

`I'(t)=12I-0.004I^2, I_o=500`

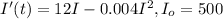
Explanation:

Population of the Community=3000

Let the number of infected=I

The number of uninfected=3000-I

The rate at which disease is spreading is proportional to the product of number of people infected and the number of people not yet infected.

`(dI)/(dt)\propto I(3000-I) \\(dI)/(dt)=k I(3000-I)\\(dI)/(dt)=0.004 I(3000-I)\\$Let I_o$=Initial Number of Infected=500\\Therefore, the initial value problem is given as:\\I'(t)=12I-0.004I^2, I_o=500`