Question

A hydrogen atom can be in the 1S state, whose energy we'll call 0, the 2S state, or any of 3 2P states. The 2S and 2P states have energies of 10.2 eV. There are other states with higher energy but we'll ignore them for simplicity. The 2P states have distinctive optical properties, so we're interested in how many are present even when it's a small fraction of the total. 1) What fraction of the H is in 2P states at T=5900 K, a typical Sun surface temperature?

Answer 1

2.02*10^-9

Step-by-step explanation:

To find the fraction of the total you use the Boltzmann's distribution:

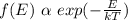`f(E)\ \alpha\ exp(-(E)/(kT))` ( 1 )

E: energy of the particle = 10.2eV = 10.2 (1.6*10^-19 J) = 1.63*10^{-18} J

K: Boltzmann's constant = 1.38*10^{-23}J/K

T: temperature of the system = 5900K

That is, the probability to find a particle with energy E is inversely proportional to e^{E/KT}.

By replacing the values of the parameters in (1) you obtain:

`f\ \alpha\ exp(-(1.63*10^(-18)J)/((1.38*10^(-23)J/K)(5900K)))=2.02*10^(-9)`

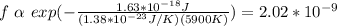
hence, approximately 2.02*10^-9 of the total hydrogen atoms are in the 2P states.