Let r represent the radius of cylinder.
We have been given that the height of a right circular cylinder is 1.5 times the radius of the base. So the height of the cylinder would be
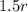 .
.
We will use lateral surface area of pyramid to solve our given problem.
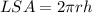 , where,
, where,
LSA = Lateral surface area of pyramid,
r = Radius,
h = height.
Upon substituting our given values in above formula, we will get:
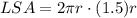
Now we will find the total surface area of cylinder.
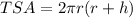
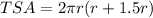
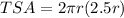
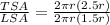
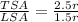
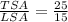
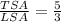
Therefore, the ratio of total surface area to lateral surface area is
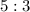 .
.