Question

The height of a right circular cylinder is 1.5 times the radius of the base. What is the ratio of the total surface area to the lateral (curved) surface area of the cylinder?

Answer 1

Let r represent the radius of cylinder.

We have been given that the height of a right circular cylinder is 1.5 times the radius of the base. So the height of the cylinder would be
`1.5r`.

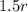We will use lateral surface area of pyramid to solve our given problem.

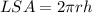`LSA=2\pi r h`, where,

LSA = Lateral surface area of pyramid,

r = Radius,

h = height.

Upon substituting our given values in above formula, we will get:

`LSA=2\pi r\cdot (1.5)r`

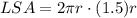
Now we will find the total surface area of cylinder.

`TSA=2\pi r(r+h)`

`TSA=2\pi r(r+1.5r)`

`TSA=2\pi r(2.5r)`

`(TSA)/(LSA)=(2\pi r(2.5r))/(2\pi r(1.5r))`

`(TSA)/(LSA)=(2.5r)/(1.5r)`

`(TSA)/(LSA)=(25)/(15)`

`(TSA)/(LSA)=(5)/(3)`

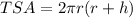
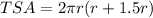
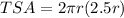
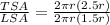
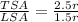
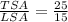
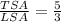
Therefore, the ratio of total surface area to lateral surface area is
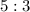`5:3`.