Question

A loud speaker has an input of 79 dB. If the volume of the sound is turned up so that the output intensity is 100 times greater, what is the new sound intensity level?​

Answer 1

99 dB

Step-by-step explanation:

To find the new sound intensity level you calculate first the initial intensity by using the following formula:

`\beta=10log((I)/(I_o))\\\\10^{(\beta)/(10)}=10^{log((I)/(I_o))}\\\\10^{(\beta)/(10)}=(I)/(I_o)\\\\I=I_o10^{(\beta)/(10)}`

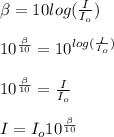
where β is the sound level of 79dB and Io is the hearing threshold of 10^-12 W/m^2. By replacing you obtain:

`I=(10^(-12)W/m^2)10^{(79)/(10)}=7.94*10^(-5)W/m^2`

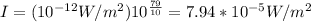
The new sound intensity level is given by:

`\beta'=10log((100I)/(I_o))=10log((100(7.94*10^(-5)W/m^2))/(10^(-12)W/m^2))\\\\\beta'=99\ dB`

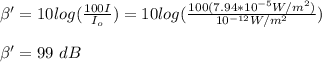
hence, the answer is 99 dB