We have been given that a normal distribution has a mean of 186.4 and a standard deviation of 48.9. We are asked to find the range of value that represents the upper 2.5% of the data.
We know that upper 2.5% of data would be 97.5% of data.
We will use z-score formula to solve our given problem.
 , where,
, where,
z = z-score,
x = Random sample score,
 = Mean,
= Mean,
 = Standard deviation.
= Standard deviation.
Now we will use normal distribution table to find z-score corresponding to 97.5% area or 0.975.
We can see from the normal distribution table that z-score corresponding to area 0.975 is
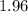 .
.
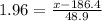
Let us solve for x.
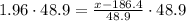

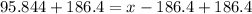
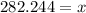
Therefore, the range
 represents the upper 2.5% of the data.
represents the upper 2.5% of the data.