Question

1. The population of a town was 500 in 2010. The population grows at a rate of 9.6% annually.

(a) Use the exponential growth model to write an equation that estimates the population t years after 2010.
(a) Estimate the population of the town in 2020. Show your work.

Answer 1

We have been given that the population of a town was 500 in 2010. The population grows at a rate of 9.6% annually.

We will use exponential growth formula to solve our given problem.

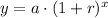`y=a\cdot (1+r)^x`, where,

y = Final amount,

a = Initial value,

r = Growth rate in decimal form,

x = Time.

Let us convert 9.6% into decimal as:

`9.6\%=(9.6)/(100)=0.096`

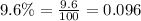
We can see that initial value is 500.

`y=500\cdot (1+0.096)^x`

`y=500\cdot (1.096)^x`

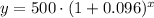
Therefore, the equation
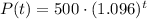`P(t)=500\cdot (1.096)^t` represents the population t years after 2010.

To find the population of the town in 2020, we will substitute
`t=10` in our equation as:

`P(10)=500\cdot (1.096)^(10)`

`P(10)=500\cdot (2.5009530650806592)`

`P(10)=1250.4765325403296\approx 1250`

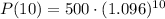
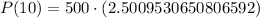
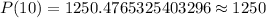
Therefore, the population of the town would be approximately 1250 in 2020.