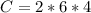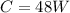Question

A power supply has an open-circuit voltage of 40.0 V and an internal resistance of 2.00 V. It is used to charge two storage batteries connected in series, each having an emf of 6.00 V and internal resistance of 0.300 V. If the charging current is to be 4.00 A, (a) what additional resistance should be added in series? At what rate does the internal energy increase in (b) the supply, (c) in the batteries, and (d) in the added series resistance? (e) At what rate does the chemical energy increase in the batteries?

Answer 1

Complete Question

A power supply has an open-circuit voltage of 40.0 V and an internal resistance of 2.00
`\Omega`. It is used to charge two storage batteries connected in series, each having an emf of 6.00 V and internal resistance of 0.300
`\Omega` . If the charging current is to be 4.00 A, (a) what additional resistance should be added in series? At what rate does the internal energy increase in (b) the supply, (c) in the batteries, and (d) in the added series resistance? (e) At what rate does the chemical energy increase in the batteries?

Answer:

a

The additional resistance is
`R_z = 4.4 \Omega`

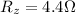
b

The rate at which internal energy increase at the supply is
`Z_1 = 32 W`

c

The rate at which internal energy increase in the battery is
`Z_1 = 32 W`

d

The rate at which internal energy increase in the added series resistance is
`Z_3 = 70.4 W`

e

the increase rate of the chemically energy in the battery is
`C = 48 W`

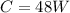
Step-by-step explanation:

From the question we are told that

The open circuit voltage is
`V = 40.0V`

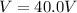
The internal resistance is
`R = 2 \Omega`

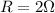
The emf of each battery is
`e = 6.00 V`

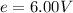
The internal resistance of the battery is
`r = 0.300V`

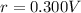
The charging current is
`I = 4.00 \ A`

Let assume the the additional resistance to to added to the circuit is
`R_z`

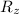
So this implies that

The total resistance in the circuit is

`R_T = R + 2r +R_z`

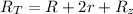
Substituting values

`R_T = 2.6 +R_z`

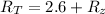
And the difference in potential in the circuit is

`E = V -2e`

=>
`E = 40 - (2 * 6)`

`E = 28 V`

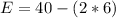
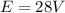
Now according to ohm's law

`I = (E)/(R_T)`

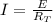
Substituting values

`4 = (28)/(R_z + 2.6)`

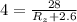
Making
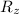`R_z` the subject of the formula

So
`R_z = (28 - 10.4)/(4)`

`R_z = 4.4 \Omega`

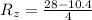
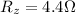
The increase rate of internal energy at the supply is mathematically represented as

`Z_1 = I^2 R`

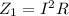
Substituting values

`Z_1 = 4^2 * 2`

`Z_1 = 32 W`

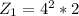
The increase rate of internal energy at the batteries is mathematically represented as

`Z_2 = I^2 r`

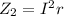
Substituting values

`Z_2 = 4^2 * 2 * 0.3`

`Z_2 = 9.6 \ W`

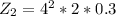
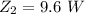
The increase rate of internal energy at the added series resistance is mathematically represented as

`Z_3 = I^2 R_z`

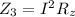
Substituting values

`Z_3 = 4^2 * 4.4`

`Z_3 = 70.4 W`

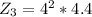
Generally the increase rate of the chemically energy in the battery is mathematically represented as

`C = 2 * e * I`

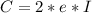
Substituting values

`C = 2 * 6 * 4`

`C = 48 W`