Answer:
a) 1.88*10^-18 N
b) 6.32*10^-19 N
c) 1.9*10^-18 N
Step-by-step explanation:
The total force over the electron is given by:
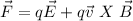
the first term is the electric force and the second one is the magnetic force.
You have that the velocity of the electron and the magnetic field are:
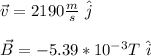
by using the relation j X (-i) =- j X i = -(-k) = k, you obtain:
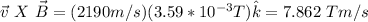
a) For an electric field of 3.91V/m in +z direction:
![\vec{F}=q[\vec{E}+\vec{v}\ X\ \vec{B}]=(1.6*10^(-19))[3.91\hat{k}+7.862\ \hat{k}]N\\\\\vec{F}=1.88*10^(-18)N\hat {k}\\\\F=1.88*10^(-18)N](https://img.qammunity.org/2021/formulas/physics/college/mna4fd4jfdqpznqrrcxx81y8zzujp0be6c.png)
b) E=3.91V/m in -z direction:
![\vec{F}=(1.6*10^(-19))[-3.91\hat{k}+7.862\ \hat{k}]N\\\\\vec{F}=6.32*10^(-19)N\hat {k}\\\\F=6.32*10^(-19)N](https://img.qammunity.org/2021/formulas/physics/college/cl5l1of48ns0cmod30221zwask2iju4kjm.png)
c) E=3.91 V/m in +x direction:
![\vec{F}=(1.6*10^(-19))[3.91\hat{i}+7.862\ \hat{k}]N\\\\\vec{F}=[6.25*10^(-19)\ \hat{i}+1.25*10^(-18)\ \hat{k} ]N\\\\F=\sqrt{(6.25*10^(-19))^2+(1.25*10^(-18))^2}N=1.9*10^(-18)\ N](https://img.qammunity.org/2021/formulas/physics/college/76v5nm6j90uchpegmprsgtedrf9ynb6hmr.png)