Answer:
The inductor contains
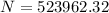 loops
loops
Step-by-step explanation:
From the question we are told that
The capacitance of the capacitor is
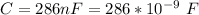
The resonance frequency is
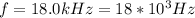
The diameter is
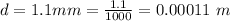
The of the air-core inductor is
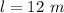
The permeability of free space is
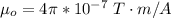
Generally the inductance of this air-core inductor is mathematically represented as

This inductance can also be mathematically represented as

Where
 is the angular speed mathematically given as
is the angular speed mathematically given as
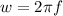
So

Now equating the both formulas for inductance
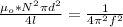
making N the subject of the formula
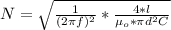
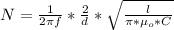
Substituting value
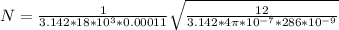
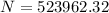 loops
loops