Question

A system executes a power cycle while receiving 1050 kJ by heat transfer at a temperature of 525 K and discharging 700 kJ by heat transfer at 350 K. There are no other heat transfers. a. Using Eq. 5.13, determine whether the cycle is internally reversible, irreversible, or impossible. b. Determine the thermal efficiency using Eq. 5.4 and the given heat transfer data. Compare this value with the Carnot efficiency calculated using Eq. 5.9 and comment.

Answer 1

(See explanation for further details).

Step-by-step explanation:

a) The real and ideal efficiencies are computed herein:

`\eta_(real) = \left(1-(Q_(out))/(Q_(in)) \right)* 100\,\%`

`\eta_(real) = \left(1-(700\,kJ)/(1000\,kJ) \right)* 100\,\%`

`\eta_(real) = 30\,\%`

`\eta_(ideal) = \left(1-(T_(L))/(T_(H)) \right)* 100\,\%`

`\eta_(ideal) = \left(1-(350\,K)/(1050\,kJ) \right)* 100\,\%`

`\eta_(ideal) = 66.667\,\%`

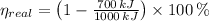
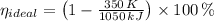
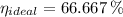
Since
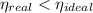`\eta_(real) < \eta_(ideal)`, the power cycle is irreversible.

b) The differences between the real and ideal efficiencies is due to the existence of irreversibilities associated to the kind of the energy transformation processes and technological issues.