We have been given two points.
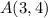 and
and
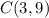 . We are asked to find the point B such that it divides line segment AC so that the ratio of AB to BC is 4:1.
. We are asked to find the point B such that it divides line segment AC so that the ratio of AB to BC is 4:1.
We will use segment formula to solve our given problem.
When a point P divides segment any segment internally in the ratio
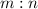 , then coordinates of point P are:
, then coordinates of point P are:
![[\right x=(mx_2+nx_1)/(m+n),y=(my_2+ny_1)/(m+n)\left]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/akyowjc7htcx82r5k6h8au77r7ufav87hh.png)
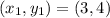 and
and
 .
.
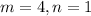
Upon substituting our given information in above formula, we will get:
![[\right x=(4(3)+1(3))/(4+1),y=(4(9)+1(4))/(4+1)\left]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/j2lfyua64e0kujm5xssjgj8tylnkufv4zv.png)
![[\right x=(12+3)/(5),y=(36+4)/(5)\left]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/s918j007i6ceri6bkxo571jauslcglxb4o.png)
![[\right x=(15)/(5),y=(40)/(5)\left]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/zzmujq44yfi1286c4pq89vudy3pbkh392e.png)
![[\right x=3,y=8\left]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dl8rh1nupeam8gtc54otvxngowq4waqwzr.png)
Therefore, the coordinates of point B would be
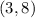 .
.