Answer:
51.02 metres
Explanation:
The pictorial representation of the problem is attached.
We are required to find the distance from the worker to the top of the pole, |DA| in the diagram.
In Triangle ABC
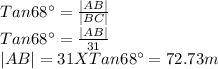
In Triangle BCD
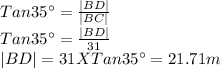
The distance, |DA| =|AB|-|BD|
=72.73-21.71
=51.02 metres
The distance from the worker to the top of the pole is 51.02 metres.