A:
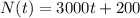
B:
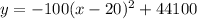
C: When they turn 18.
A. Write a linear function N(t) for the amount of money, N, that Nat has in her account ‘t’ years after her 5th birthday:
You can determine a linear equation using the two coordinates provided:
(2, 6200) and (5, 21200).
To do this, first find the slope of the graph. You can do this by using the expression
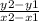 , where the coordinate (2, 6200) is 1 and (7, 21200) is 2:
, where the coordinate (2, 6200) is 1 and (7, 21200) is 2:
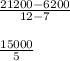
The slope is equal to 3000. Now, you need to find the y-intercept. Plug in 2 for x and see what the y intercept would need to be to equal 6200:
6200 = 3000 * 2 + b
6200 = 6000 + b
b = 200
Thus, your equation for Nat's bank account is
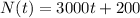
B: Kat’s account doesn’t follow a linear model, but rather a quadratic model. On her 5th birthday, her parents open the account and then add money annually just like with Nat. Kat’s parents plan is to add money so that her account maxes out at $44100 on her 25th birthday. At the age of 14, she has $32000. Write a quadratic function K(t) for the amount of money, K, in Kat’s account ‘t’ years after her 5th birthday:
The question supplies you with the vertex to the parabola, (20, 44100). This is the point at which the maximum value of the function is reached.
It also supplies you with a point on the parabola, (9, 32000).
You can use the vertex form of the quadratic equation to find the formula for Kat's bank account:
 , where (h, k) is the vertex.
, where (h, k) is the vertex.
Substituting the vertex in for that equation, we get:
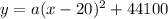
Now, you can substitute the point (14, 32000) in for x and y to solve for a:
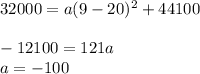
Thus, the equation is
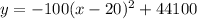 .
.
C. What age will both Nat and Kat have the same amount in their account? 18 years old.
To find what age each account will be equal, set the equations equal to each other:
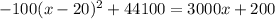
Then, you can solve for x:
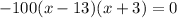
Solving for x, we notice that the accounts equal each other when Nat and Kat are -3 or 13. However, Nat's function is only specified to begin after she turns 5, so add 5 to 13 to get 18.
They will both have the same money in their accounts when they turn 18.