Answer:
The probability that a randomly selected monthly cell phone bill is less than $95 is 0.9772
Explanation:
The average monthly household cellular phone bill is $73.

Local monthly household cell phone bills are normally distributed with a standard deviation of $11.

We are supposed to find the probability that a randomly selected monthly cell phone bill is less than $95 i.e.P(x<95)
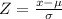
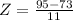
Z=2
Refer the z table for p value
So,p value = 0.9772
Hence the probability that a randomly selected monthly cell phone bill is less than $95 is 0.9772