Question

In a double‑slit interference experiment, the wavelength is λ = 452 nm λ=452 nm , the slit separation is d = 0.190 mm d=0.190 mm , and the screen is D = 49.0 cm D=49.0 cm away from the slits. What is the linear distance Δ x Δx between the eighth order maximum and the third order maximum on the screen?

Answer 1

Δx = 5.82mm

Step-by-step explanation:

To find the distance between the eight maximum and the third one you use the following formula:

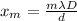`x_m=(m\lambda D)/(d)` (1)

λ: wavelength = 452*10^-9 m

m: order of the fringes

D: distance to the scree = 0.49m

d: distance between slits = 0.190*10^-3 m

you use for m=8 and m=3, then you calculate x8 - x3:

`x_8=(8(452*10^(-9)m)(0.49m))/(0.190*10^(-3)m)=9.32*10^(-3)m\\\\x_3=(3(452*10^(-9)m)(0.49m))/(0.190*10^(-3)m)=3.49*10^(-3)m\\\\\Delta x_(8,3)=5.82*10^(-3)m=5.82mm`

hence, the distance between these fringes is 5.82mm