We have been given that Willy has compounded monthly to invest his summer earnings of $4259 in the Rock Solid Bank. The bank is offering 6%. We are asked to find the amount of money will be after 5 years.
We will use compound interest formula to solve our given problem.
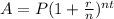 , where,
, where,
A = Final amount after t years,
P = Principal amount,
r = Annual interest rate in decimal form,
n = Number of times interest is compounded per year.
t = Time in years.
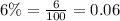
Since interest is compounded monthly, so
 and
and
 .
.

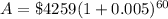
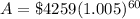

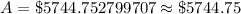
Therefore, Will will have approximately
 in 5 years.
in 5 years.