Answer:
a. $1251.5
b. $1254.64
c. 15.4 years
d. 30.56 years
Explanation:
Given the information:
- Principle (P) = $800
- Interest = 4.5%
As we know, the formula to find the future value of Jackie deposit with interest is compounded monthly, quaterly, ..is
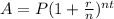 where:
where:
- P = initial balance
- r = interest rate (decimal)
- n = number of times compounded annually
- t = time
Hence:
a. If the interest is compounded quarterly how much money will Jackie have in 10 years?
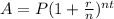
<=>
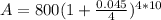
<=> A = $1251.5
d. If Jackie's money is compounded monthly, how long will it take her money to triple?
<=>
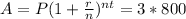
<=>

<=>
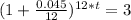
<=> t = 30.56 years
As we know, the formula to find the future value of Jackie deposit with interest is compounded continuously
A = P*
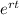 where e is the mathematical constant approximated as 2.7183.
where e is the mathematical constant approximated as 2.7183.
b. If the interest is compounded continuously how much money will Jackie have in 10 years?
<=> A = 800*
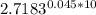
<=> A = $1254.64
C. If Jackie's money is compounded continuously, how long will it take her money to double?
<=> P*
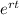 = 2*800
= 2*800
<=> 800*
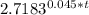 = 1600
= 1600
<=>
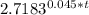 = 2
= 2
<=> t = 15.4 years