Answer:
The number of molecules in the volume is
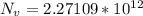 molecules
molecules
Step-by-step explanation:
From the question we are told that
The pressure of the ultrahigh vacuum is

The molecular diameter of the gas molecules

The temperature is
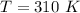
Avogadro's number is
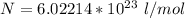
The volume of the gas is
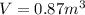
From the ideal gas law[
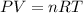 ] that the number of mole is mathematically represented as
] that the number of mole is mathematically represented as
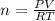
Where R is the gas constant with a value
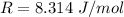
Substituting values

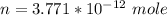
The number of molecules is mathematically represented as
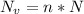
Substituting values
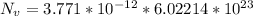
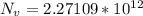 molecules
molecules