Answer:
(A)He multiplied the equation
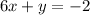 by –5 incorrectly.
by –5 incorrectly.
Explanation:
To solve the system of linear equations:
Part of Amos' calculations is shown:
8 x + 5 y = 18.
6 x -5 y = 10.
When you multiply 6x+y =-2 by -5, we have the expression:
This was not Amos' result as he got 6 x -5 y = 10.
Therefore, he multiplied the equation
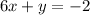 by –5 incorrectly.
by –5 incorrectly.
The correct option is A.