We have been given that a parabola has vertex
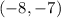 and also passes through the point
and also passes through the point
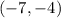 . We are asked to write the equation of the parabola in vertex form.
. We are asked to write the equation of the parabola in vertex form.
We know that vertex form of parabola in format
 , with a vertex at point (h,k).
, with a vertex at point (h,k).
Let us write equation of parabola using our given information as:
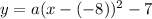
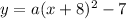
Now we will substitute the coordinates of point
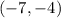 to solve for a as:
to solve for a as:
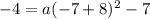
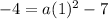

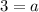
Therefore, our required equation would be
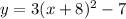 .
.