We have been given that in ΔHIJ, the measure of ∠J=90°, the measure of ∠I=29°, and JH = 88 feet. We are asked to find the length of IJ to the nearest tenth of a foot.
First of all, we will draw a right triangle using our given information as shown in the attachment.
We can see that in triangle HIJ, the side IJ is adjacent side to angle I and JH is opposite side to angle I.
We know that tangent relates opposite side of right triangle to adjacent side.
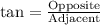
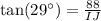
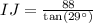
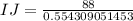

Upon rounding to nearest tenth, we will get:
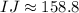
Therefore, the length of the side IJ is approximately 258.8 units.