Step-by-step explanation :
Here, A right angled triangle is given with the measure of two sides and we are to find the measure of the third side.
We'll find the measure of third side with the help of the Pythagorean theorem,
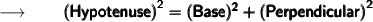
Here,
- The perpendicular (AB) is 28 in

So, substituting the values in the formula we get :
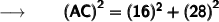
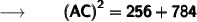

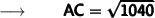
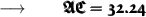
Therefore,
- The length of the hypotenuse (AC) is 32.2 in (Rounded to nearest tenth)