Question

Boyle's Law states that when a sample of gas is compressed at a constant temperature, the pressure P and volume V satisfy the equation PV = C, where C is a constant. Suppose that at a certain instant the volume is 600 cm3, the pressure is 150 kPa, and the pressure is increasing at a rate of 40 kPa/min. At what rate is the volume decreasing at this instant?

Answer 1

The volume is decreasing at 160 cm³/min

Step-by-step explanation:

Given;

Boyle's law, PV = C

where;

P is pressure of the gas

V is volume of the gas

C is constant

Differentiate this equation using product rule:

`V(dp)/(dt) +P(dv)/(dt) = (d(C))/(dt)`

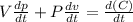
Given;

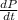`(dP)/(dt)` (increasing pressure rate of the gas) = 40 kPa/min

V (volume of the gas) = 600 cm³

P (pressure of the gas) = 150 kPa

Substitute in these values in the differential equation above and calculate the rate at which the volume is decreasing (
`(dv)/(dt)`);

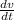(600 x 40) + (150 x
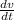`(dv)/(dt)`) = 0

`(dv)/(dt) = -((600*40))/(150) = -160 \ cm^3/min`

Therefore, the volume is decreasing at 160 cm³/min