Question

A manufacturer of a new medication on the market for Crohn's disease makes a claim that the medication is effective in 85% of people who have the disease. One hundred seventy-five individuals with Crohn's disease are given the medication, and 135 of them note the medication was effective. Does this finding provide statistical evidence at the 0.05 level that the effectiveness is less than the 85% claim the company is making? Make sure to include parameter, conditions, calculations, and a conclusion in your answer. (10 points)

Answer 1

We conclude that the effectiveness is less than the 85% claim the company is making.

Explanation:

We are given that a manufacturer of a new medication on the market for Crohn's disease makes a claim that the medication is effective in 85% of people who have the disease.

One hundred seventy-five individuals with Crohn's disease are given the medication, and 135 of them note the medication was effective.

Let p = percentage of people who have the Crohn's disease.

So, Null Hypothesis,
`H_0` : p = 85% {means that the effectiveness is equal to the 85% claim the company is making}

Alternate Hypothesis,
`H_A` : p < 85% {means that the effectiveness is less than the 85% claim the company is making}

The test statistics that would be used here One-sample z proportion statistics;

T.S. =
`\frac{\hat p-p}{\sqrt{(\hat p(1-\hat p))/(n) } }` ~ N(0,1)

where,
`\hat p` = sample proportion of individuals who note the medication was effective =
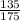`(135)/(175)` = 0.77

n = sample of individuals with Crohn's disease taken = 175

So, test statistics =
`\frac{0.77-0.85}{\sqrt{(0.77(1-0.77))/(175) } }`

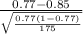
= -2.515

The value of z test statistics is -2.515.

Now, at 0.05 significance level the z table gives critical value of -1.645 for left-tailed test.

Since our test statistic is less than the critical value of z as -2.515 < -1.645, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region due to which we reject our null hypothesis.

Therefore, we conclude that the effectiveness is less than the 85% claim the company is making.