We have been given that a sprinkler is designed to rotate 360∘ clockwise, and then 360∘ counterclockwise to water a circular region with a radius of 11 feet. The sprinkler is located in the middle of the circular region. The sprinkler begins malfunctioning and is only able to rotate 225∘ in each direction.
We are asked to find the area of the sector to nearest square foot.
We will use area of sector formula to solve our given problem.
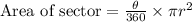 , where,
, where,
 = Central angle of sector,
= Central angle of sector,
 = Radius.
= Radius.
For our given problem
 and
and
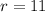 .
.
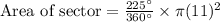
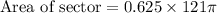
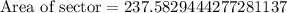
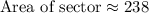
Therefore, the sprinkler can water approximately 238 square feet.