Answer:
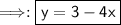
Explanation:
To solve for y, you have to isolate it on one side of the equation.
12x+3y=9
First, you have to subtract by 12x from both sides.
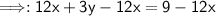
Solve.
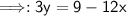
Then, you divide by 3 from both sides.
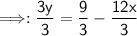
Solve.
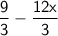
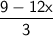
Use the distributive property.
⇒A(B+C)=AB+AC
9-12x=3(3-4x)
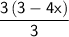
Divide the numbers from left to right.
3/3=1
3-4x
Then, rewrite the problem down.
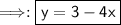
- Therefore, the correct answer is y=3-4x.
I hope this helps! Let me know if you have any questions.