Answer:
The p value for this test is given
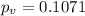
Since the p value is higher than the significance level given of
 we have enough evidence to FAIL to reject the null hypothesis. And we can say that the true proportion of firms in the manufacturing sector still do not offer any child-care benefits to their workersis is not significantly higher than 0.85 or 85% at 5% of significance.
we have enough evidence to FAIL to reject the null hypothesis. And we can say that the true proportion of firms in the manufacturing sector still do not offer any child-care benefits to their workersis is not significantly higher than 0.85 or 85% at 5% of significance.
Explanation:
We define the proportion of interest as p who represent the true proportion of firms in the manufacturing sector still do not offer any child-care benefits to their workers
And we want to anaylze the following system of hypothesis:
Null hypothesis:
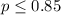
Alternative hypothesis:
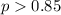
And the statistic for this test is given by:
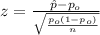
The p value can be calculated with this formula:
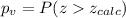
And the p value for this test is given
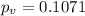
Since the p value is higher than the significance level given of
 we have enough evidence to FAIL to reject the null hypothesis. And we can say that the true proportion of firms in the manufacturing sector still do not offer any child-care benefits to their workersis is not significantly higher than 0.85 or 85% at 5% of significance.
we have enough evidence to FAIL to reject the null hypothesis. And we can say that the true proportion of firms in the manufacturing sector still do not offer any child-care benefits to their workersis is not significantly higher than 0.85 or 85% at 5% of significance.