Question

Help? I can't seem to understand arithmegic sequence.

Answer 1

A sequence
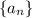`\{a_n\}` is arithmetic if the difference between consecutive terms is some fixed number, regardless of which pair of consecutive terms you pick out of the sequence.

For example, the following sequences are arithmetic:

1, 2, 3, 4, 5, 6, ... (difference = 1)

-25, -20, -15, -10, -5, ... (difference = 5)

2. Carla's sequence is not arithmetic, because the differences between consecutive terms are all different:

13 - 11 = 2

17 - 13 = 4

25 - 17 = 8

She can adjust the sequence by changing the last two numbers to 15 and 17, since this makes the difference fixed:

13 - 11 = 2

15 - 13 = 2

17 - 15 = 2

and so on.

3. The sequence

45, 48, 51, 54, ...

is arithmetic with difference 3 between terms. Recursively, we can write the
`n`th term,
`a_n`, in terms of the previous,
`(n-1)`th term,
`a_(n-1)`:

`a_n=a_(n-1)+3`

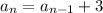
By this definition, we can just as easily write the
`(n-1)`th term in terms of the
`(n-2)`th term:

`a_(n-1)=a_(n-2)+3`

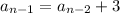
Then, substituting this into the previous equation, we have

`a_n=(a_(n-2)+3)+3=a_(n-2)+2\cdot3`

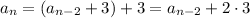
We can continue this process to write
`a_n` in terms of
`a_1`:

`a_(n-2)=a_(n-3)+3\implies a_n=a_(n-3)+3\cdot3`

`a_(n-3)=a_(n-4)+3\implies a_n=a_(n-4)+4\cdot3`

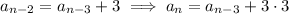
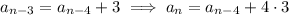
and so on. (You might notice that the subscript of the term on the right side, and the number of 3s being added, together sum to
`n`.) The pattern continues down to

`a_n=a_1+(n-1)\cdot3`

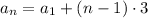
The first term in this sequence is
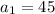`a_1=45`, so we have

a.
`a_n=45+3(n-1)=42+3n`

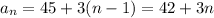
where
`n=1,2,3,\ldots`.

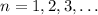b. You can fill in the blanks by just adding 3 to the previous term:

45, 48, 51, 54, 57, 60, 63, 66, 69, ...

Then, using the formula found in (a), the 15th term of the sequence is

`a_(15)=42+3\cdot15=87`