Answer:
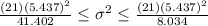

And the confidence interval for the deviation would be obtained taking the square root of the last result and we got:
3.9<σ<8.8
Explanation:
Data given:
65.2 71.9 72.8 73.1 73.1 73.5 75.5 75.7 75.8 76.1 76.2 76.2 77.0 77.9 78.1 79.6 79.7 79.9 80.1 82.2 83.7 93.8
The sample mean would be given by:

We can calculate the sample deviation with this formula:
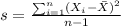
And we got:
s=5.437 represent the sample standard deviation
 represent the sample mean
represent the sample mean
n=22 the sample size
Confidence=99% or 0.99
The confidence interval for the population variance is given by:

The degrees of freedom given by:
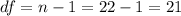
The Confidence is 0.99 or 99%, the value of significance is
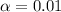 and
and
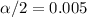 , and the critical values are:
, and the critical values are:
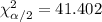
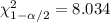
And the confidence interval would be:
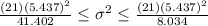

And the confidence interval for the deviation would be obtained taking the square root of the last result and we got:
3.9<σ<8.8