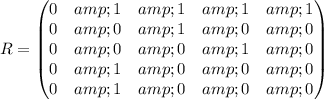Question

4. Determine which of the following relations on the given sets are reflexive, symmetric, antisymmetric and/or transitive: a) ℛ = {(1,5), (5,1), (1,1), (2,2), (3,3)(4,4)} oooo ???????? = {1,2,3,4,5} Write the matrix representation of this relation. b) ???????? = {(1,4), (1,2), (2,3), (3,4), (5,2), (4,2), 1,3)} oooo ???????? = {1,2,3,4,5} Write the matrix representation of this relation.

Answer 1

(a)

Reflexivity

Is not reflexive

Symmetry

Is symmetric

Anti-Symmetry

is not antisymmetric.

Transitivity

It is transitive

`R = \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\0 & 1 & 0 & 0 & 0 \\0 & 0& 1 & 0 & 0 \\0 & 0& 0 & 1 & 0 \\0 & 0& 0& 0 & 1 \end{pmatrix}`

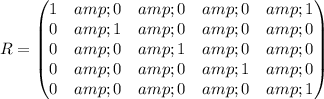
(b)

Reflexivity

Is not reflexive

Symmetry

Is not symmetric

Anti-Symmetry

It is antisymmetric

Transitivity

So is NOT transitive.

`R = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 \\0 & 0 & 1 & 0 & 0 \\0 & 0& 0 & 1 & 0 \\0 & 1& 0 & 0& 0 \\0 & 1& 0& 0 & 0 \end{pmatrix}`

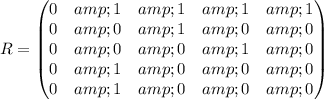
Explanation:

(a)

Reflexivity

Is not reflexive because 5 is not related to 5.

Symmetry

Is symmetric because 1R5 .and 5R1

Anti-Symmetry

If it is symmetric then it is not antisymmetric.

Transitivity

It is transitive because 1R5 5R1 and 1R1.

`R = \begin{pmatrix} 1 & 0 & 0 & 0 & 1 \\0 & 1 & 0 & 0 & 0 \\0 & 0& 1 & 0 & 0 \\0 & 0& 0 & 1 & 0 \\0 & 0& 0& 0 & 1 \end{pmatrix}`

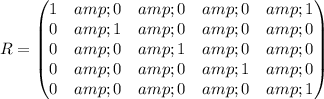
(b)

Reflexivity

Is not reflexive no element of the set is related to itself.

Symmetry

Is not symmetric because (1,4) belongs to the relation but (4,1) does not belong to the relation . And similarly you can do the same with all pairs and none of them will satisfy the condition.

Anti-Symmetry

It is symmetric because for every element if aRb then "b" is NOT related to "a"

Transitivity

A relation can't be antisymmetric and transitive. So is NOT transitive.

`R = \begin{pmatrix} 0 & 1 & 1 & 1 & 1 \\0 & 0 & 1 & 0 & 0 \\0 & 0& 0 & 1 & 0 \\0 & 1& 0 & 0& 0 \\0 & 1& 0& 0 & 0 \end{pmatrix}`