Question

An SAT coaching company claims it's course can raise SAT scores of high school students (thus, when they take it a second time after being coached). Of course, students who retake the SAT without paying for coaching generally raise their scores also. A random sample of students who took the SAT twice found 427 who were coached and 2733 who were not coached. For both the coached group and the uncoached group, the gain in score was recorded. The SAT coaching company wishes to test to see if their coaching provided better second attempts on average. What case is best

Answer 1

Check the explanation

Explanation:

(a) The appropriate test is the matched-pairs test because a student’s score on Try 1 is certainly correlated with his/her score on Try 2. Using the differences, we have xbar = 29 and s = 59.

(b) To test H0: mu=0 vs. H1 mu > 0, we compute

`t = (29-0)/((59/sqrt(427))=10.16`

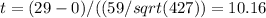
with df = 426. This is certainly significant, with P < 0.0005. Coached students do improve their scores on average

(a) H0: μ1 = μ2 vs. Ha: μ1 > μ2, where μ1 is the mean gain among all coached students and μ2 is the mean gain among uncoached students. H0 and Ha. Using the conservative approach, df = 426 is rounded down to df = 100 in (t table) and we obtain 0.0025 < P < 0.005. Using software, df = 534.45 and P = 0.004. There is evidence that coached students had a greater average increase.

(b) 8 ± t*(3.0235) where t* equals 2.626 (using df = 100 with (t table) ) or 2.585 (df = 534.45 with software). This gives either 0.06 to 15.94 points, or 0.184 to 15.816 points, respectively.

(c) Increasing one’s score by 0 to 16 points is not likely to make a difference in being granted admission or scholarships from any colleges.