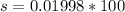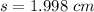Question

A wire loop with 60 turns is formed into a square with sides of length s . The loop is in the presence of a 1.20 T uniform magnetic field B⃗ that points in the negative y direction. The plane of the loop is tilted off the x-axis by θ=15∘ . If i=2.50 A of current flows through the loop and the loop experiences a torque of magnitude 0.0186 N⋅m , what are the lengths of the sides s of the square loop, in centimeters?

Answer 1

2 cm

Step-by-step explanation:

To fins the lengths of the sides of the loop you use the following formula for the calculation of the torque experienced by the loop in a magnetic field:

`\tau=NiABsin\theta`

N: turns of the loop = 60

i: current in the loop = 2.50A

A: area of the loop = s*s

B: magnitude of the magnetic field = 1.20T

θ: angle between the plane of the lop and the direction of B = 15°

BY replacing the values of the torque and the other parameters in (1) you can obtain the area of the loop:

`A=(\tau)/(NiBsin\tetha)=(0.0186Nm)/((60)(2.5A)(1.2T)sin15\°)=3.99*10^(-4)m^2`

but the area is s*s:

`A=√(s)=\sqrt{3.99*10^(-4)m^2}=0.019m\approx2cm`

hence, the sides of the square loop have a length of 2cm

Answer 2

the length of the sides s is
`s = 1.998 \ cm`

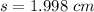
Step-by-step explanation:

From the question we are told that

The number of turns is
`N = 60 \ turn`

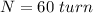
The magnetic field is
`B = 1.20 \ T`

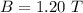
The angle the loop makes with the x-axis
`\theta = 15 ^o`

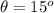
The current flowing through the loop is
`I = 2.50 A`

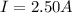
The magnitude of the torque is
`\tau = 0.0186 \ N`

the length of the sides of the square is
`s`

Generally, we can represent the torque magnitude as

`\tau = N I A B sin \theta`

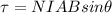
Where A is the area of the square which is mathematically represented as

`A = s^2`

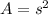
Substituting this into the formula for torque

`\tau = N I s^2 B sin \theta`

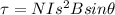
making s the subject

`s = \sqrt{(\tau )/(NIB sin \theta ) }`

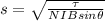
Substituting values

`s = \sqrt{(0.0186)/((60) * (2.50) * (1.20) * (sin (15))) }`

`s = 0.01998 m`

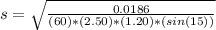
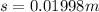
Converting to centimeters

`s = 0.01998 * 100`

`s = 1.998 \ cm`