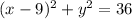Question

Answer and how to do it

Answer 1

`(x - 9)^2 + y^2 = 36`

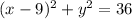
Explanation:

The equation of a circle in standard form is

`(x - h)^2 + (y - k)^2 = r^2`

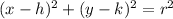
You are given

`x^2 + y^2 - 18x + 45 = 0`

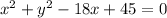
In order to put the equation in standard from, we need to complete the square. Since there is no y term, the y part is simply y^2, and there is no need to complete the square for y. For x, we do have an x term, so we must complete the square in x.

Start by grouping the x terms and subtracting 45 from both sides.

`x^2 - 18x + y^2 = -45`

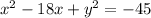
Now we need to complete the square for x.

`x^2 - 18x ~~~~~~+ y^2 = -45`

The number that completes the square will go in the blank above, and it will also be added to the right side of the equation.

To find the number you need to add to complete the square, take the coefficient of the x term. It is -18. Divide it by 2. You get -9. Now square -9 to get 81. The number that completes the square in x is 81. Now you add it to both sides of the equation.

`x^2 - 18x + 81 + y^2 = -45 + 81`

`(x - 9)^2 + y^2 = 36`

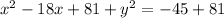
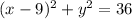
Answer:
`(x - 9)^2 + y^2 = 36`