Answer:
468 m
Step-by-step explanation:
So the building and the point where the laser hit the water surface make a right triangle. Let's call this triangle ABC where A is at the base of the building, B is at the top of the building, and C is where the laser hits the water surface. Similarly, the submarine, the projected submarine on the surface and the point where the laser hit the surface makes a another right triangle CDE. Let D be the submarine and E is the other point.
The length CE is length AE - length AC = 284 - 234 = 50 m
We can calculate the angle ECD:
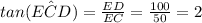

This is also the angle ACB, so we can find the length AB:
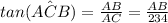
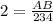
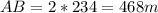
So the height of the building is 468m