Question

In a large class of introductory Statistics​ students, the professor has each person toss a fair coin 1111 times and calculate the proportion of his or her tosses that were heads. The students then report their​ results, and the professor plots a histogram of these several proportions. ​a) What shape would you expect this histogram to​ be? Why? ​b) Where do you expect the histogram to be​ centered? ​c) How much variability would you expect among these​ proportions? ​d) Explain why a Normal model should not be used here.

Answer 1

Given:

Sample size, n = 11

P = 0.5

a) The shape of the histogram will be symmetrical. This is because the probability of getting heads and tails is equal.

b) The histogram is centered at

p = 0.5 (because of equal probability of obtaining heads and tails).

c) How much variability would you expect among these​ proportions?

Here, we are to find the standard deviation.

Let's use the formula:

`\sigma = \sqrt{(pq)/(n)}`

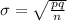
Where

p = 0.5(probability of getting heads)

q = 0.5 (probability of getting tails)

Therefore

`\sigma = \sqrt{(0.5 * 0.5)/(11)}`

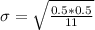
= 0.0227 ≈ 0.023

The standard deviation is 0.023

d) A normal model should not be use here because the success/failure condition is violated, since each student only flips the coin 11 times, it impossible to obtain both at least 10 heads and at least 10 tails. Here, the sample size is too small.