Question

According to a Gallup survey conducted in July 2011, 20% of Americans favor reducing the U.S. budget deficit by using spending cuts only, with no tax increases. An economics professor believes that fewer college students would favor deficit reduction through spending cuts only. The professor surveys 500 college students and finds that 75 of them favor reducing the deficit using only spending cuts. What is the test statistic?

Answer 1

The test statistic is
`t = -62.5`

Explanation:

The null hypothesis is:

`H_(0) = 0.2*500 = 100`

The alternate hypotesis is:

`H_(1) < 0.2*500 < 100`

Our test statistic is:

`t = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

In this problem:

`X = 75, \mu = 100, \sigma = √(500*0.8*0.2) = 8.94, n = 500`

So

`t = (75 - 100)/((8.94)/(√(500)))`

`t = -62.5`

The test statistic is
`t = -62.5`

Answer 2

`z=\frac{0.15 -0.2}{\sqrt{(0.2(1-0.2))/(500)}}=-2.795`

Explanation:

Data given by the problem

n=500 represent the random sample taken

X=75 represent the students in favor to reducing the deficit using only spending cuts

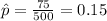`\hat p=(75)/(500)=0.15` estimated proportion of favor to reducing the deficit using only spending cuts

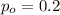`p_o=0.2` is the value that we want to check

z would represent the statistic

System of hypothesis

We want to cehck if the true proportion of students in favor to reducing the deficit using only spending cuts is less than 0.2.:

Null hypothesis:
`p\geq 0.2`

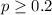
Alternative hypothesis:
`p < 0.2`

The statistic for this case is given by:

`z=\frac{\hat p -p_o}{\sqrt{(p_o (1-p_o))/(n)}}` (1)

Replacing the info provided we got:

`z=\frac{0.15 -0.2}{\sqrt{(0.2(1-0.2))/(500)}}=-2.795`