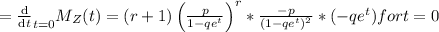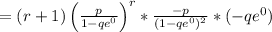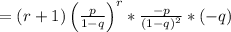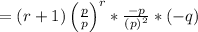Question

The number of withdrawals a bank processes in a day follows a random variable X. The number of deposits in a day is represented by Y. X and Y are independent and have the following moment generating functions \displaystyle {M}_{X}(t)=\frac{p}{1-q{e}^{t}} \displaystyle {M}_{Y}(t)={\left(\frac{p}{1-q{e}^{t}}\right)}^{r} q = 1 - p What is the expected number of transactions in a day?

Answer 1

Check the explanation

Explanation:

Number of transactions in a day is sum of number of withdrawals and number of deposits. So,

Number of transactions in a day, Z = X + Y

Moment Generating function of Z is,

T+1

Expected number of transactions in a day = E[Z]

`= \frac{\mathrm{d} }{\mathrm{d} t}_(t=0)M_Z(t) = (r+1)\left ( (p)/(1-qe^t) \right )^(r) * (-p)/((1-qe^t)^2) * (-qe^t) for t = 0`

`= (r+1)\left ( (p)/(1-qe^0) \right )^(r) * (-p)/((1-qe^0)^2) * (-qe^0)`

`= (r+1)\left ( (p)/(1-q) \right )^(r) * (-p)/((1-q)^2) * (-q)`

`= (r+1)\left ( (p)/(p) \right )^(r) * (-p)/((p)^2) * (-q)`

`= ((r+1)q)/(p)`